Tree Decomposition: Generalizing Tree-Based Positional Encodings to General Graphs
In the last few years, graph transformers have emerged as a powerful architecture to handle graph data. One crucial factor underpinning their success is the use of positional and structural encodings. Without these encodings, transformers are unable to extract anything about the actual structure of the graph and would solely rely on the nodes' features. In order to make graph transformers exploit the graph structure properly, one thus needs to add informative structural and positional encodings to the node features.
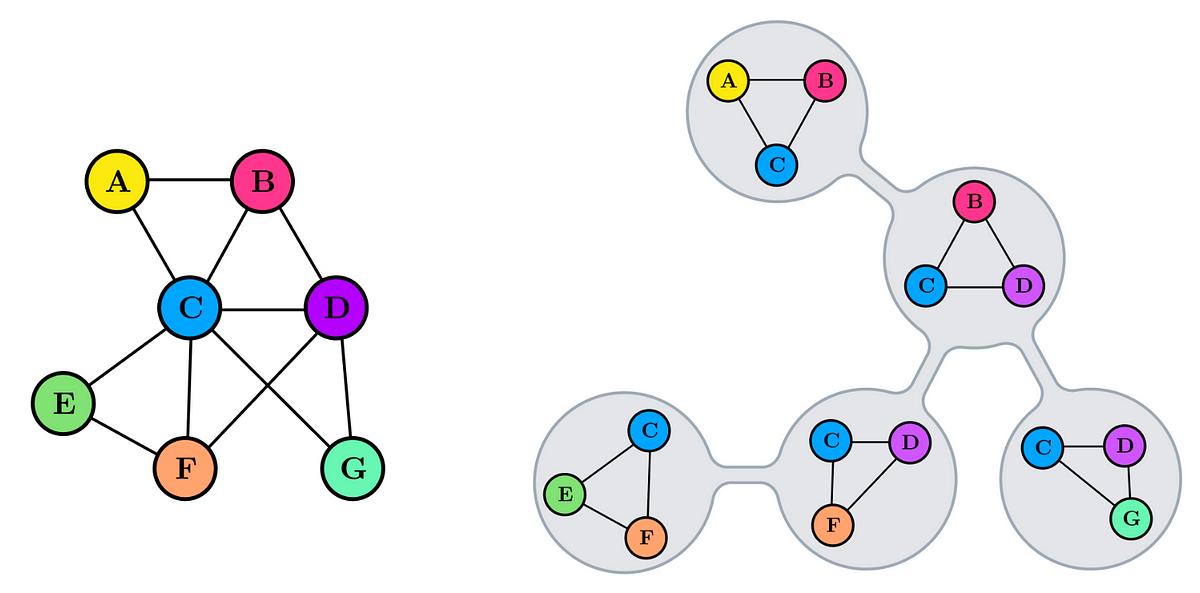
In this project, the central idea revolves around tree decompositions, particularly utilizing treewidth (a notion from graph theory) as a foundation to derive a new positional encoding with theoretical founding. Treewidth is a combinatorial metric that measures how close a given graph is to being a tree. For example, a tree has treewidth 1 while a fully connected graph is as far as possible from being a tree and has treewidth |V|. A cycle is somewhere in the middle and has treewidth 2. In practice, most graphs are rather sparse and come with a low treewidth of at most 5. The second ingredient is a positional encoding that explicitly works for trees. The aim of this project is now to use the underlying tree of the graph (as given by the tree decomposition) as the basis to generalize that positional encoding from trees to general graphs.
This new positional encoding should then be empirically evaluated on several practical datasets with the help of graph transformers.
Prerequisites:
- Familiarity with or strong interest in graph theory
- Solid programming skills in python
- At least basic knowledge in machine learning and deep learning
Literature
Novel positional encodings to enable tree-based transformers
